이번 포스트에서는 학습 프로세스의 마지막 단계인 3단계, 모델 업데이트 방법을 소개하고자 한다. 모델 업데이트는 학습 결과와 실제 정답을 비교하여 모델을 평가한 다음, 그에 맞는 피드백을 제공하여 실제 정답에 근접한 모델을 찾아가기 위해 필요한 과정이다.

모델은 간단히 말해 변수들 간의 관계식이다. 중학교 수학에서 배웠던 방정식은 \(y=Wx+b\) 이라는 관계식이 정해져 있고, 관계식에 따라 y에 상응하는 x값을 찾는 것이었다. 기계학습은 반대로 (x, y)의 데이터가 주어졌을 때 이 둘의 관계를 가장 잘 설명하는 W와 b 값을 귀납적인 방법으로 찾아간다. 지난 포스트에서 다뤘던 손실함수를 사용해서 손실함수의 값을 최소화하는 방향으로 가중치를 바꿔가면 정답에 근접한 관계식을 찾을 수 있다.
다시 중학교 수학으로 돌아가보자. 어떤 함수의 최소값/최대값은 그래프의 기울기가 0인 지점이다. 그렇다면 손실함수 그래프에서도 기울기가 0인 지점을 계산하면 쉽게 정답을 찾을 수 있지 않을까? 변수가 한 두개 정도인 간단한 모델이라면 단순 계산으로 최소값을 찾을 수 있겠지만, 그렇다면 기계학습을 공부하는 의미가 없을 것이다. 기계학습을 사용해서 찾고자 하는 모델은 보통 변수가 굉장히 많고, 변수 간의 관계가 복잡하기 때문에 계산으로 한번에 최소값을 찾는 것이 거의 불가능하다.
손실함수 그래프 전체적인 모양은 계산할 수 없다고 해도 현재 위치에서의 순간기울기(Gradient)는 미분으로 알 수 있기 때문에 그 위치에서 조금씩 아래로 내려가다(Descent)보면 기울기가 0인 지점이 나오지 않을까 하는 것이 이번 포스트에서 설명할 경사하강법(Gradient Descent)의 기본 아이디어이다.
경사하강법
변수가 하나인 경우
변수가 하나인 가장 단순한 모델을 통해 경사하강법을 이해해보자.
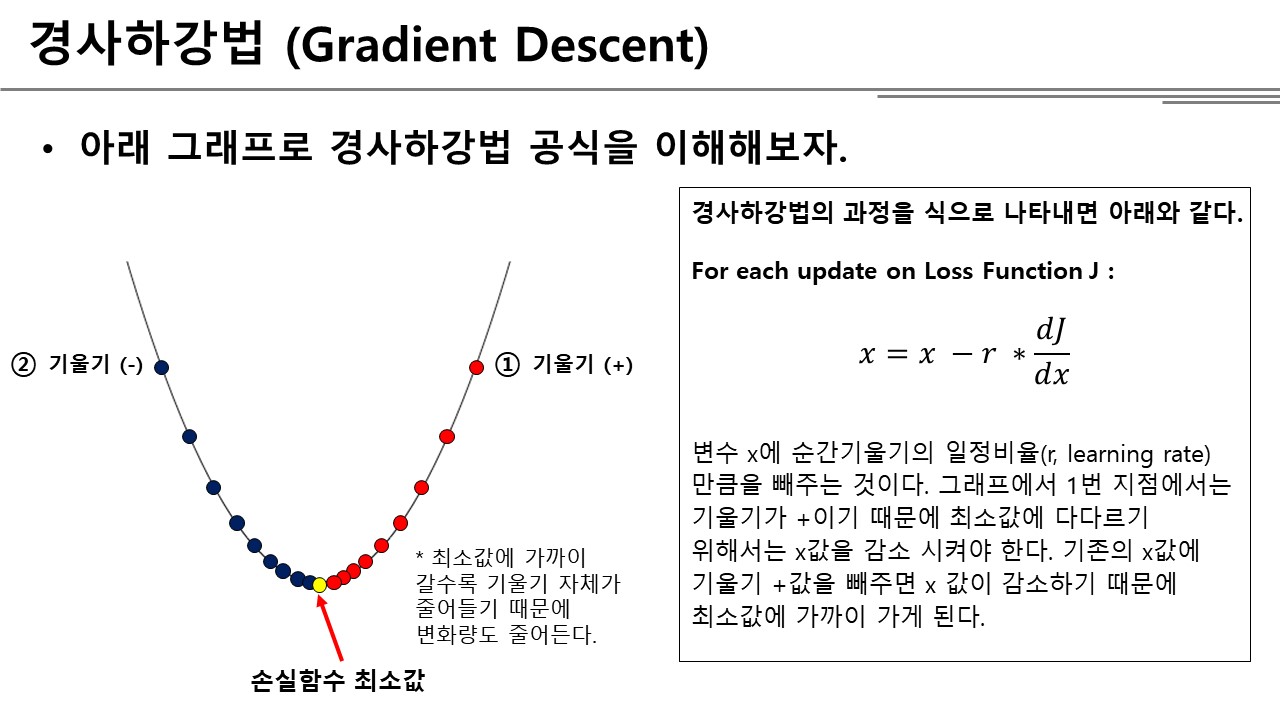
앞서 설명했듯이 경사하강법은 매 업데이트마다 순간기울기의 일정 비율만큼 움직인다. 이것을 식으로 나타내면 아래와 같다.
\(\large {x=x-\gamma \ast \frac { dJ }{ dx } }\)
현재 위치의 순간기울기는 손실함수 J에 대해 x의 미분으로 구할 수 있고, 기존의 변수 x에 순간기울기의 일정비율(learning rate) 만큼을 빼주면 다음 학습에 사용할 x값이 업데이트 된다. 이 식이 유효한 이유는 무엇인지는 그래프를 보면 쉽게 이해할 수 있다.
눈을 가린 상태에서 산을 내려간다고 상상해보자. 나는 현재 나의 위치에 대한 정보만 있을 뿐, 산이 전체적으로 알 수 없다. 그렇다고 산을 내려갈 수 없는 것은 아니다. 현재 나의 위치에서 발의 감각으로 오르막인지, 내리막인지 알 수 있기 때문에 내리막길의 방향으로 한발짝씩 움직이면 산을 내려갈 수 있다.
경사하강법도 마찬가지이다. 우리가 찾아가야 하는 지향점은 손실함수 J의 값이 최소인 즉, 기울기가 0인 지점이다. 하지만 그래프 전체의 모양은 알 수 없기 때문에 그래프 상 현재 위치에서 내리막이 어딘지를 찾고 내리막 방향으로 조금씩 움직여 보는 것이다. 그래프에서 오른쪽과 같이 순간기울기가 양수인 경우라면 뒤로 가야 내리막이기 때문에 기존 변수 x 값에 기울기만큼 빼주면 골짜기에 가까워지고 반대로 순간기울기가 음수인 경우라면 앞으로 가야 내리막이기 때문에 변수 x에 기울기만큼 더해주면(음수만큼 빼주면) 골짜기에 가까워진다.
Learning Rate, r
식에서 나오는 \(\gamma\)는 learning rate라고 하는 값인데, 한발짝을 기울기에 비례해서 얼마나 크게 내딛을지 결정하는 값이다. 대담한 사람이라면 내리막 방향으로 크게 한발짝 내딛을 것이고, 신중한 사람이라면 종종걸음으로 내려갈 것이다. learning rate은 최소값을 찾아가는 효율과도 관련이 있는데, 종종걸음으로 내려가는 것이 훨씬 더 정확하게 골짜기를 찾아갈 수는 있지만 걸음수와 시간은 많이 들 것이고, 큰 걸음으로 내려간다면 시간은 훨씬 덜 들 수 있지만, 골짜기에 가까이 가서는 계속 반대쪽 등성이로 발을 내딛어 골짜기 자체에는 다다르지 못하는 경우(수렴하지 못하고 발산하는 경우)가 발생할 수 있다. 따라서 적당한 Learning Rate을 결정하는 것도 기계학습에서 중요한 이슈이다(대부분의 예제에서는 0.1을 사용한다).
변수가 여러 개인 경우
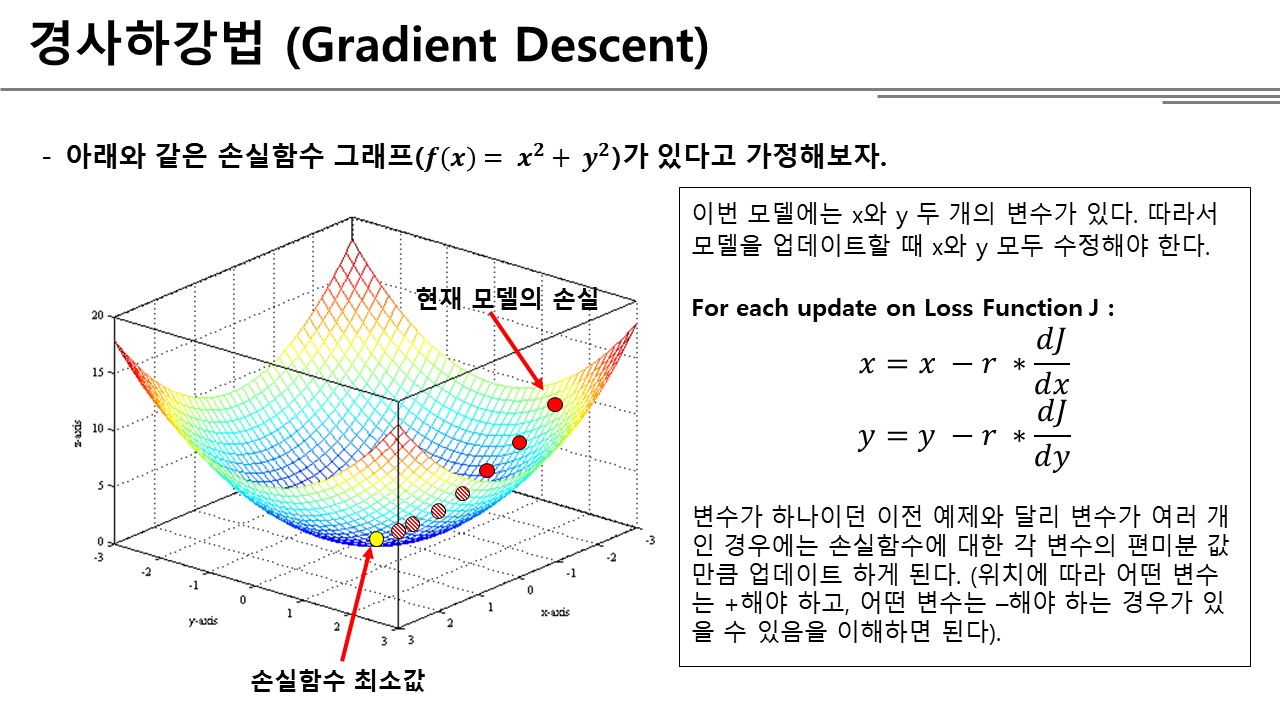
변수가 여러 개인 경우의 경사하강법도 원리는 동일하다. 다만 매 업데이트마다 각 변수들의 값을 모두 수정해주면 된다. 그래프 상에서 보듯이 변수가 여러 개인 경우 손실함수의 그래프는 2차원 이상으로 나타나고, 그마저도 3차원 이상인 경우에는 그래프로 표현할 수 없다. 연역적인 방법으로 최소값을 찾을 수 없기 때문에 경사하강법이 절실하다.
변수가 여러 개인 경우는 변수 하나인 경우에 소개했던 식을 각 변수에 적용하면 된다.
변수 업데이트 과정을 파이썬 코드로 나타내면 다음과 같다.
"""
function : 미분을 구할 함수
x : 편미분 기준 변수
x의 위치에서 순간기울기를 구하는 함수
함수에 따라서 편미분 식이 달라지기 때문에 General하게 사용하기 위해
x를 기준으로 작은 값 h만큼 위아래로 움직였을 때의 기울기를 계산한다.
"""
def derivative(function, x):
h = 1e-4
return (function(x+h) - function(x-h)) / 2*h
"""
model : 모델에서 사용하는 변수 값 리스트
loss_function : 손실함수
model 변수에는 모델에서 사용하는 변수의 값들이 들어있고, 본 함수에서는 그 값들을 돌아가면서 업데이트하여 리턴한다.
업데이트하는 방식은 위에서 설명하였듯이 기존의 값에서 순간기울기 만큼을 빼는 방식을 사용한다.
learning_rate은 default 0.1로 적용하였다.
"""
def gradient_descent_with_derivative(model, loss_function, learning_rate = 0.1) :
for param in model :
model[param] -= derivative(loss_function, model[param])
return model

