10강 벡터의 직교성과 직선투영
이번 장의 목표
- 벡터이 직교하는 조건에 대해 알아본다.
- Orthogonal Complement의 조건과 4가지 부벡터공간의 관계를 알아본다.
- 직선 투영에 대해 알아본다.
한양대 이상화 교수님의 오픈 강의로 공부한 내용을 정리한 것입니다. 강의 영상과 강의 노트는 다음 링크에서 다운받아 작성하였습니다.
http://www.kocw.net/home/search/kemView.do?kemId=977757
Orthogonality
벡터의 직교성
- 벡터
x와y가 직교하는 조건은 피타고라스의 정리를 통해 유도할 수 있다. ▶x와 y의 내적이 0일 때 - N개의 벡터가 서로 직교할 때, 벡터는 서로 독립적이다.
- 서로 직교하는 Basis를 사용하여 벡터 공간을 정의하면 연산이 훨씬 간편해진다.
Subspace의 직교성
- 벡터 뿐만 아니라 Subspace끼리도 직교할 수 있다.
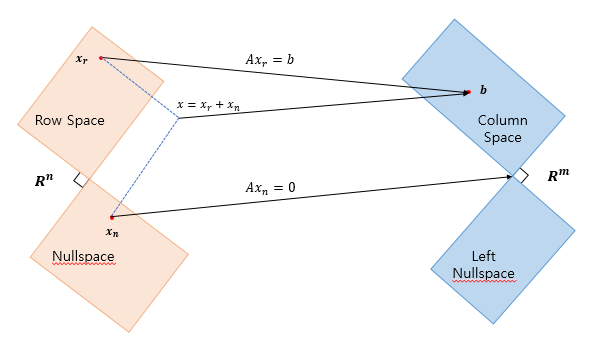
Subspace 𝑆1의 모든 벡터가 또 다른 Subspace 𝑆2의 모든 벡터에 수직일 때, 𝑆1과 𝑆2는 직교 한다.- 4가지 부벡터공간에서 다뤘던 Column Space - Left Nullspace, Row Space - Nullspace의 관계의 연장
C(A) ⊥ N(AT)C(AT) ⊥ N(A)
Orthogonal Complement
- 부벡터공간에는 직교성 말고도 특별한 성질이 있는데,
Dim(C(A))+ Dim(N(AT)) = mDim(C(AT)) + Dim(N(A)) = n
- 이렇게 서로 직교하면서, 차원의 합이 전체 벡터 공간을 이루는 두 공간을
Orthogonal Complement하다고 한다. - 4가지 부벡터공간의 관계를 그림으로 표현하면 아래와 같다.
Projection
- 직선 a(또는 subspace S)에서 벡터 b와 가장 가까운 점을 찾는 과정을 Projection(투영)이라고 한다. 결국 벡터 b에서 a로 수선의 발을 내리는 과정이다.
- 벡터 a와 b의 내적값은 a로부터 b에 내린 Projection 값으로 이해할 수 있다.
- Projection의 문제는
Ax=b연립방정식의 해가 존재하지 않을 때, 최적의 해(최소의 error)를 찾는 과정에서 자주 활용된다.
Projection matrix : P
- Projection 과정도 행렬 P로 표현할 수 있다.
- Projection Matrix P는 벡터 a의 성분으로만 이루어졌기 때문에 P는 a의 multiplication으로 이해할 수 있다.
- 당연히 Projection point p도 a의 multiplication한 값이다.

