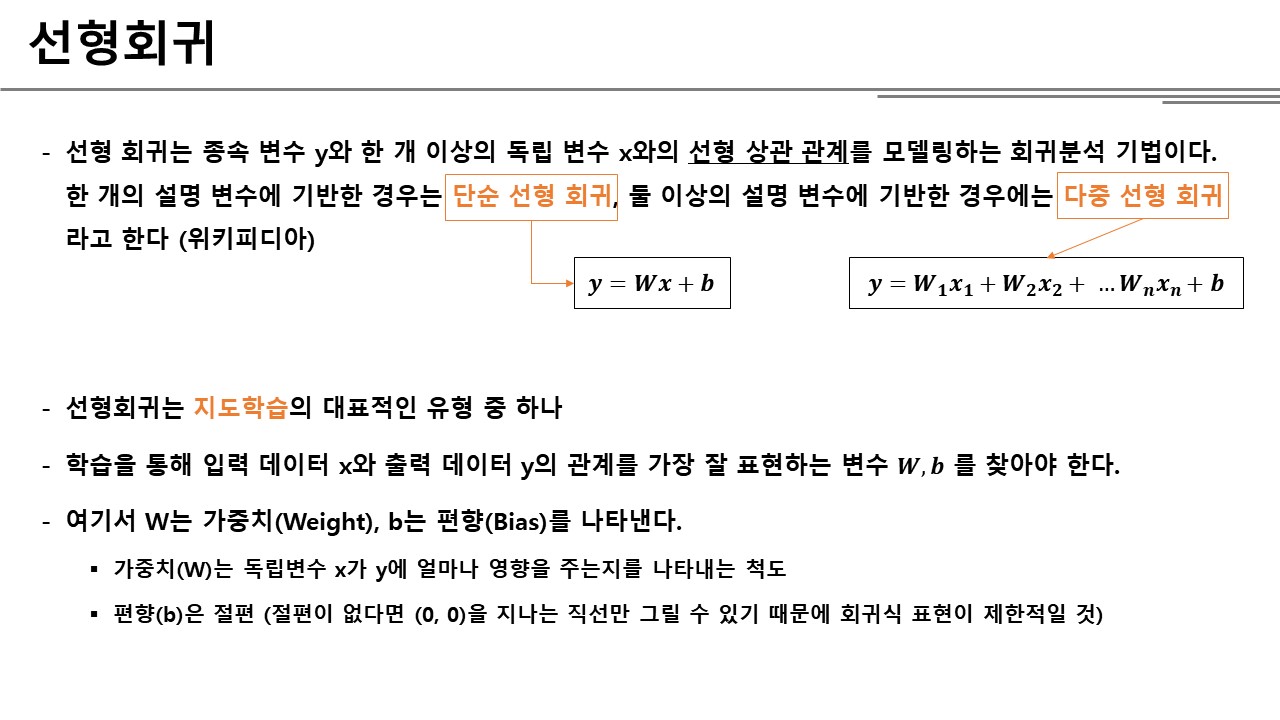
선형회귀모델
이번 포스트부터는 드디어 실제로 기계학습에서 사용되는 모델들과 적용 방법들을 다룰 것이다. 어느 입문서에서든 가장 먼저 설명하는 모델이 선형회귀모델인데, 여러 모델 중에서 가장 이해하기 쉽고, 간단한 모델이기 때문이다.
통계학개론을 배운 사람이라면 기본적인 회귀분석 모델에 대한 지식은 있을테지만, 간단히 설명하자면 종속변수 X와 독립변수 Y의 n차 관계식을 찾는 모델이라고 생각하면 된다. 함수식을 찾는다고 생각하면 될 것이다. 회귀분석 모델에서 가장 많이 언급되는 것이 바로 이번 포스트에서 설명할 선형회귀 모델인데, 이름에서도 나타나듯이 X와 Y의 관계를 선형으로 나타내는 모델을 의미한다. 선형이라는 것은 간단히 1차식으로 표현한다고 이해하면 된다.
아래와 같은 데이터가 있다고 가정해보자.
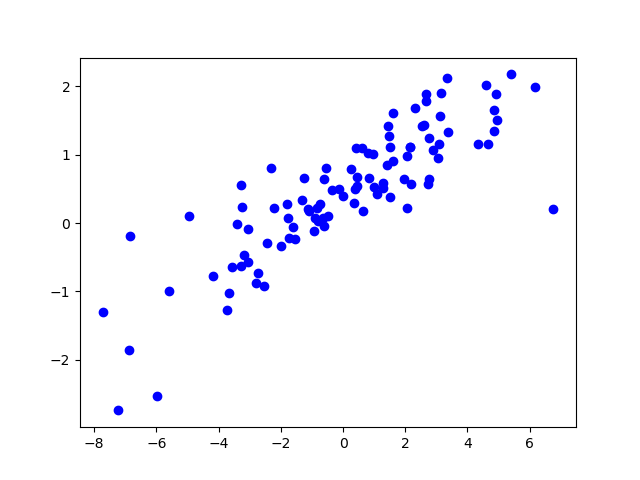
가로축 X와 세로축 Y가 정확히 어떻게 관계인지는 몰라도 X와 Y를 어느정도 직선으로 표현할 수 있다는 것은 눈치챌 수 있다. 선형회귀모델은 X와 Y의 관계를 가장 잘 나타내는 직선을 찾아내는 과정이다.
선형회귀 모델은 크게 두가지로 나뉘는데, 설명 변수 X가 하나인 경우는 단순선형회귀, 여러 개인 경우는 다중선형회귀라고 한다. 선형회귀 모델은 X와 Y의 관계를 1차식으로 나타내는 것이기 때문에 두 경우 모두 간단히 아래와 같은 식으로 표현할 수 있다.
\({y=Wx+b}\)
다만, 단순선형회귀의 경우는 x 위치에 하나의 실수가 들어가고, 다중선형회귀는 여러 실수를 담은 벡터가 들어간다(자세한 내용은 마지막 챕터에서 다루는 것으로 한다). 식에서 W는 가중치(Weight)로 결과값 Y에 설명변수 X가 얼마나 영향을 주는지 나타낸다. b는 편향(또는 오차항)을 나타내는데, X만으로 설명할 수 없는 모든 오차값들을 표현한다.
기계학습을 통해서 우리는 X와 Y의 관계를 가장 잘 표현하는 관계식을 찾는다는 것은, 결국 가장 적절한 W와 b값을 찾는다는 것을 의미한다.
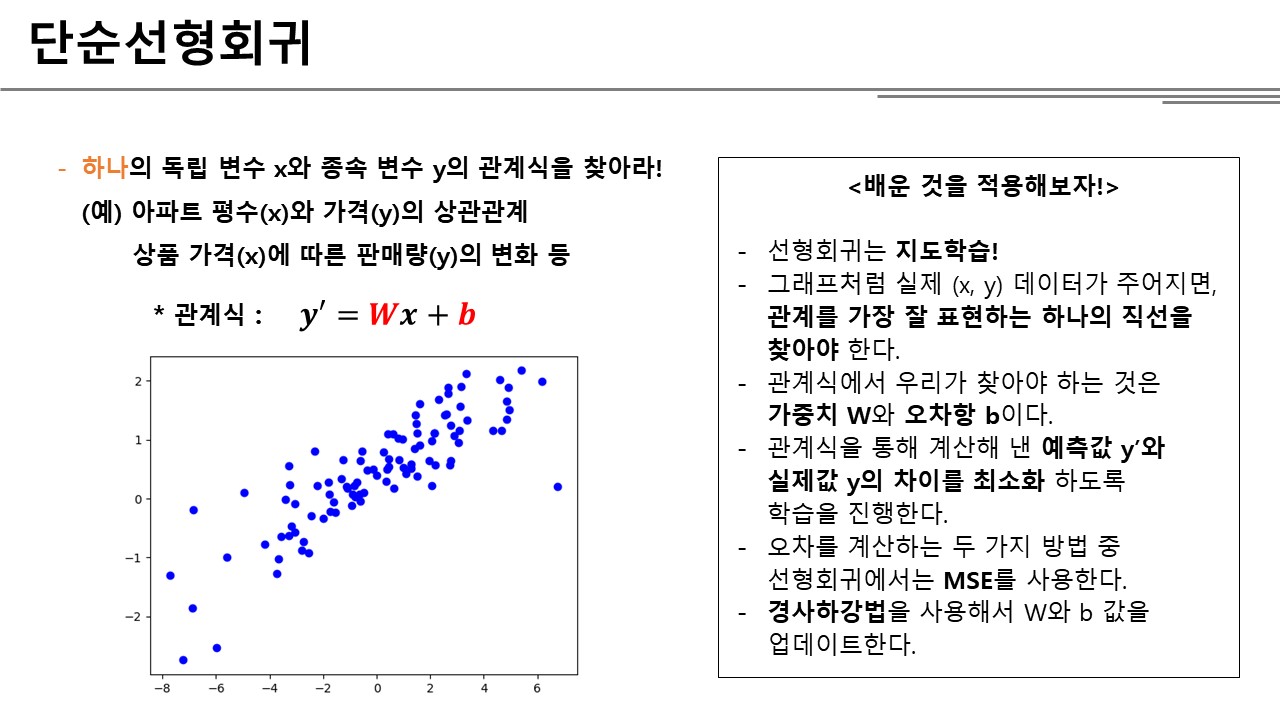
단순선형회귀
단순선형회귀는 결과값 Y에 영향을 미치는 변수가 하나라는 가정이다. 위에서 본 그래프와 같이 하나의 X와 대응되는 Y값이 주어질 때 둘의 관계를 찾는 것이다. 따라서 W와 b 값은 모두 하나의 실수로 구성된다. 학습의 결과는 \({y’=0.5x+3}\) 과 같이 최종 W와 b 값으로 대치된 하나의 식으로 나타날 것이다.
그렇다면 가장 적절한 W와 b 값은 어떤 과정을 찾아내는 것일까? 지난 포스트까지 설명했던 학습과정을 그대로 적용하면 된다.
- 모델(또는 가설)을 세워서 적용하고,
- 세운 가설을 평가하고,
- 평가를 바탕으로 가설을 업데이트한다.
여기서 ‘모델’이라고 한 것은 특정한 W와 b값을 적용한 관계식인데, 위의 과정을 우리가 알고 있는 과정에 대입하면 아래와 같다.
- \({y’=0.5x+3}\)라는 모델을 가지고 예측값 y’를 계산한다.
- MSE를 사용하여 실제값 y와 예측값 y’의 오차를 계산한다.
- 오차에 따라 경사하강법으로 W와 b 값을 업데이트한다.
실제 데이터에 적용해보자. 먼저 예제에 사용할 (x, y) 데이터쌍 200개를 생성한다.
import numpy as np
def create_dataset() :
data_size = 200
dataset = []
for i in range(data_size):
x = np.random.normal(0.0, 0.55)
y = x * 0.1 + 0.3 + np.random.normal(0.0, 0.03)
dataset.append((x, y))
x_data = [v[0] for v in dataset]
y_data = [v[1] for v in dataset]
return (x_data, y_data)
첫번째 Iteration을 위해 W와 b의 초기값을 설정한다. 보통 W값은 랜덤으로, b값은 0으로 시작한다.
model = {}
model['W'] = np.random.random()
model['b'] = 0
(x_data, y_data) = create_dataset()
x_data = np.array(x_data) # 일반 파이썬 리스트에서 numpy array로 변환
y_data = np.array(y_data)
위에서 설명한 세가지 과정을 코드로 표현해보자.
# 1. 현재의 모델로 예측값 y'를 계산
def predict(model):
global x_data
return x_data * model['W'] + model['b']
# 2. 오차 계산 (MSE)
def mean_squared_error(model):
print("MSE model : ")
print(model)
global x_data
global y_data
y_predict = predict(model) # 현재의 가설을 바탕으로 x 데이터에 대한 예측값 y를 리턴하는 함수
m = x_data.shape[0] # 훈련 데이터의 개수
mse = 1 / (2 * m) * np.sum((y_predict - y_data)**2)
print("loss : ", mse)
return mse
# 편미분 계산
def derivative(function, model) :
h = 1e-4
grads = {}
for param in model:
temp = model
temp[param] = model[param] + (2*h)
plus = function(temp)
# 원래는 (+h ~ -h) 한 값의 기울기를 구하는 게 더 정확하다
grads[param] = (plus - function(model)) / (2*h)
return grads
# 3. 경사하강법으로 변수 업데이트
def gradient_descent_with_derivative(loss_function, learning_rate=0.1):
global model
grads = derivative(loss_function, model)
# 편미분 구한 값을 learning rate만큼 반영하여 업데이트
for param in model:
model[param] -= (learning_rate * grads[param])
# 실제로 테스트해보자
# 100번을 실험하면서 W와 b 값이 어떻게 변화하는지 살펴본다
iteration = 100
for i in range(iteration):
gradient_descent_with_derivative(mean_squared_error)
print("model : ")
print(model)
실험을 하면서 주의깊게 봐야하는 값은 사실 Loss이다. 학습의 목표가 Loss 값을 최소화하는 것임을 기억하면, Iteration이 계속되면서 Loss 값이 점점 커지는 상황이 발생했을 때, learning rate을 조절해서 Loss가 발산하지 않도록 수정해야 한다. Learning Rate은 W와 b 값을 업데이트 할 때 한번에 움직이는 보폭을 얼마나 크게 할 것인지 결정하는 변수이다. Loss 값이 발산한다는 것은 한번에 너무 많이 움직인다는 것을 의미하기 때문에 이럴 때는 Learning Rate을 더 작게 해서 보폭을 작게 만들어야 한다.
Tensorflow 이용해서 구현하기
사실 파이썬만으로도 기계학습 알고리즘을 구현할 수는 있지만 위에서 보듯이 코드가 복잡해지고 작성자가 신경써야할 부분도 많아진다. 그래서 보통 기계학습 알고리즘을 적용할 때 본인이 직접 모든 코드를 구현하기 보다 미리 만들어져 있는 소스를 활용하는데 가장 많이 사용되는 것이 구글에서 제공하는 Tensorflow이다. Tensorflow를 활용하면 Gradient Descent나 Loss 계산 이런 것들을 미리 만들어져있는 함수에 맡기고 우리는 틀만 짜주면 된다.
Tensorflow를 활용하면 위의 복잡한 코드가 아래처럼 간단해진다. 물론 그 전에 Tensorflow 패키지를 모두 설치해야 한다.
import tensorflow as tf
import numpy
(x_data, y_data) = create_dataset()
x_data = np.array(x_data)
y_data = np.array(y_data)
# Tensorflow를 사용할 때는 학습을 진행하기 전에
# 먼저 어떠한 방식으로 학습시킬지 변수들을 먼저 설정해주어야 한다.
# 설정해야 하는 변수에는 관계식 W와 b, Loss 함수, 최적화 방식 등이 있다.
# tf.Variable() 함수는 학습시켜야 하는 변수를 만들어 준다.
# 여기서 W와 b는 모두 실수 하나로 구성된다.
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
b = tf.Variable(tf.zeros([1]))
# x와 y의 관계식을 설정한다.
y = W * x_data + b
# loss는 실제값 y_data와 예측값 y의 MSE를 구하는 방식으로 설정
loss = tf.reduce_mean(tf.square(y - y_data))
# 최적화는 우리가 배운 Gradient Descent 방식을 사용한다.
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.5)
# 학습은 loss로 설정한 MSE를 minimize(최소화) 하는 방식으로 사용한다.
train = optimizer.minimize(loss)
# 여기까지는 학습 변수 설정이고
# 실제 학습은 Session 안에서 이루어진다.
with tf.Session() as sess :
sess.run(tf.global_variables_initializer()) # 변수 W, b 초기화
for i in range(iteration):
sess.run(train)
print(i, sess.run(W), sess.run(b))
# 그래프 출력
plt.plot(x_data, y_data, 'ro')
plt.plot(x_data, sess.run(W) * x_data + sess.run(b))
plt.legend()
plt.show()
Loss 함수나 최적화 함수를 직접 작성할 때보다 코드가 훨씬 간결해졌다. Tensorflow를 활용하면 우리는 학습이 진행되면서 나오는 결과 분석에만 신경쓰면 되고, 나머지는 Tensorflow에 맡겨두면 된다. 앞으로 예제 코드는 Tensorflow를 사용하는 버전으로 작성하도록 하고, 우리는 원리를 이해하는 데 집중하도록 하자.