Logistic Regression에 신경망 적용하기 (1)
Binary Classification
Logistic Regression은 보통 Yes or No 문제를 정의할 때 사용한다. 어떤 사진을 주고 고양이 사진인지 아닌지를 판단한다든지, 스팸 메일인지 아닌지 판단하는 등의 문제를 떠올리면 된다.
고양이 사진을 추려내는 문제가 있다고 가정해보자. 우리에게 64x64 크기의 사진이 주어질 것이고, 각 픽셀은 RGB 값으로 나타낸다. 우리의 학습 모델에서 Input Layer는 64x64x3의 픽셀 색상 정보가 될 것이고, Output Layer는 0 / 1이 될 것이다.
M개의 데이터가 있고, 각 X가 N개의 요소로 구성되어 있다고 하면, {(X1, Y1), (X2, Y2), … (Xm, Ym)}으로 나타낼 수 있고, 이것을 한 행렬로 나타내면 X = ‘[X1;X2; … ;Xm’] ‘(N x M 행렬’), Y = ‘[Y1; Y2; … ;Ym’]이 된다.
Logistic Regression
X가 주어졌을 때 Yes or No로 결과를 얻기 위해서는 어떤 식으로 식을 설계해야할까? 결과값 Y를 P(y=1 | X), 즉, X(Input)가 주어졌을 때 결과가 1일 확률이라고 정의하면 Y값이 우리가 가진 기준보다 높을 때 고양이일 것이라고 판단할 수 있다.
저 확률은 어떻게 구할까? X와 Y의 관계식을 가장 간단하게 1차식으로 정의하면 t = wX + b이 되고, X는 N x M 행렬이기 때문에 W는 N차 행렬로 정의할 수 있다.
위의 식으로 구한 t의 값을 0 <= Y <= 1 이도록 하기 위해서 Sigmoid 함수를 사용하는데, 식과 그래프는 다음과 같다.
\(sig(t)=\frac{1}{1+e^(-t)}\)
(Sigmoid 함수 그래프 삽입)
위의 식에서 t에 해당하는 것이 wX + b이고 Y = sig(wX + b)로 정의할 수 있다.
Cost Function
우리가 참에 가까운 관계식을 찾아가기 위해서 w와 b를 계속해서 바꿔나가면서 학습을 할텐데, 지금의 관계식이 다른 것들보다 효과적인 모델인지 아닌지 판단할 수 있는 기준이 필요하다. 머신러닝에서는 Cost Function을 판단 기준으로 삼는다. 즉, 이 식으로 학습을 시킬 때의 Cost, 비용이 얼마나 드는지를 계산하는 것인데, 여기서 Cost란 참값과 예측값 사이의 차이의 합(Training Set이 여러개이기 때문에)이다. 쉽게 말해, 우리가 식을 가지고 도출해낸 예측값과 실제의 y값들의 차이가 적으면 적을수록 효과적인 모델을 찾아낸 것이라고 생각할 수 있다. 각 Training Set에서의 비용을 계산하는 식을 Loss(Error) Function이라고 하는데,
Linear Regression에서는 아래와 같은 식으로, \( L(X, Y) = ((wX+b)-Y)^2)\)
Logistic Regression에서는 아래의 식을 사용한다.
\(L(y, Y) = -(Ylogy + (1-Y)log(1-y))\) (y는 예측값, Y는 참값이라고 하자)
선형회귀와 달리 Logistic 회귀에서 이런 괴상한 식이 나오게 된 이유를 찬찬히 생각해보자. Loss Function의 기능은 예측값과 참값의 차이를 계산하는 것이기 때문에, 예측값과 참값이 다르면 값이 커지고, 같으면 값이 작아져야 한다. 그런데 Logistic Regression은 선형회귀분석과 달리 y값의 범위가 0과 1 사이로 한정되어 있기 때문에 기존의 것을 그대로 사용할 경우 함수의 결과값이 차이를 드러내는 데에 효과적이지 않다. 그래서 좀 더 극적으로 예측값과 참값의 차이를 드러내기 위해서 위와 같은 Loss Function을 고안하게 된 것이다.
생각해보자. Y = 1이라고 하면 L = -logy가 될 것이고, L의 값이 작아지기 위해서는 y 값이 커야하고, y가 1일 때 가장 크다. 반대로 Y = 0이라고 하면 L = -log(1-y)이고, L의 값이 작아지기 위해서는 마찬가지로 1-y의 값이 커야하고, y가 0일 때 가장 크다. 위의 Loss Function은 예측값과 참값이 같을 때 가장 작은 값을, 다를 때 가장 큰 값을 리턴하는 아주 효과적인 함수인 것이다.
각각의 Training Set에 대해 Loss를 구하면 그것을 다 더한 값이 Cost Function의 결과가 된다(내가 지금 가지고 있는 모델의 Cost).
\( Cost(w, b) = \frac{1}{M}sum(L(y, Y))\)
Gradient Descent
Cost Function 구하는 식을 왜 배운 것일까? 이걸로 우리는 무엇을 할 수 있을까? 기계학습에서 ‘학습’이란 무엇인가? 하는 질문들은 결국에는 Cost Function으로 귀결된다. Cost Function의 결과는 현재 내가 가지고 있는 관계식(wX+b)를 바탕으로 내가 예측한 y값과 참값 Y 사이의 오차를 의미한다. 우리가 학습을 통해 좀 더 나은 예측을 한다는 것은 결국 예측값과 참값의 오차가 작아야 한다는 의미이고, 우리는 Cost Function의 결과값을 최소로 하는 w와 b 값을 찾아야 하는 것이다.
우리 학습의 목표는 Cost를 최소로 하는 w와 b를 찾는 것!!
그런데 Cost Function은 정적인 값, 현재 내가 들고 있는 w, b 값으로 얻어낸 결과이기 때문에 결과가 충분히 좋은 것인지 아니면 더 좋아질 수 있는지 알 수 없다. 결국 w, b 값을 요리조리 바꿔가면서 가장 최적의 값을 찾아가야 하는데, 이런 방법을 Gradient Descent라고 한다. 말 그대로 기울기를 따라 Cost를 내려가는 것이다.
앞서 설명하였듯이 Gradient Descent(경사하강법)은 Cost Function, J(w, b) 함수의 최적값을 찾아가기 위한 방법이다.
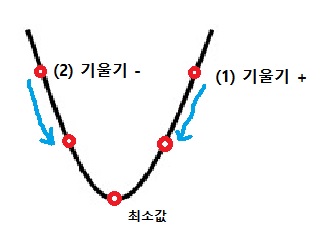
위의 그림은 간단하게 2차함수로 경사하강법의 원리를 설명한 것이다. 그래프를 변수 w에 따른 Cost Function의 변화 그래프라고 가정해보자. 우리는 w값을 조정해가면서 가장 아래에 있는 최소값에 도달해야 한다. 그런데 현재 우리가 (1)지점에 있다고 가정하면, w값을 점점 줄여가야만 최소값에 도달할 수 있다. 반대로 (2)지점에 있을 때는 w값을 점점 키워가야만 최소값에 도달할 수 있다. 우리는 최소값을 가지는 w값이 무엇인지 모르기 때문에 그래프 상에서 어디에 있든지 한번에 한발짝씩 옮겨가면서 왼쪽으로 이동할지, 오른쪽으로 이동할지 결정해야만 한다. 그럼 한번에 이동할 양을 어떻게 정할까? Gradient Descent라는 이름에서도 알 수 있듯이 한번에 순간 기울기만큼 이동하기로 정한다.
즉, 한번 w값을 옮길 때마다 \( w = w - alpha * \frac{dJ(w)}{dw}\) 만큼씩 w값에 변화를 주는 것이다. 이 식이 위에서 우리가 그림으로 이해한 것과 맞아떨어지는지 살펴보자. (1)지점에서는 기울기, 곧 \(\frac{dJ(w)}{dw}\)가 (+)이기 때문에 변화한 w값은 이전보다 왼쪽으로 이동한다. 반대로 (2)지점에서는 기울기가 (-)이기 때문에 (-) x (-) = (+)가 되어 w값은 증가하게 된다. 여기에서 alpha라고 하는 값을 기울기에 곱해주는데 alpha는 learning rate이라고 하며 이동하는 보폭을 조정하는 역할을 한다. learning rate이 너무 작은 값을 가지면 한번 움직일 때마다 종종걸음으로 이동하기 때문에 최소값을 찾는데 너무 많은 연산을 거쳐야 하고, 반대로 너무 큰 값을 가지면 한번 움직일 때마다 최소값을 그냥 지나쳐버려 값을 찾는데에 실패할 가능성이 있다. 그렇기 때문에 상황에 맞는 적절한 learning rate을 정하는 것 역시 학습에서 중요한 역할을 한다.

